Quick-Start Guide: Quantum Image Representation with piQture

Hello readers,

A couple of weeks ago I defended my Master’s thesis titled piQture: A Quantum Machine Learning (QML) Library for Image Processing¹. Encouraged by the response and interest in piQture, I am here with a series of quick-start guides to the library.

Introducing piQture

piQture is a Python and Qiskit-based software framework designed to accommodate users familiar with classical machine learning but without prior experience in QML. It provides users with an accessible workflow to design, implement, and experiment with QML models for real-life applications such as image processing.

Quantum Image Representation (QIR)

Today, I wish to dive into one of piQture’s standout features implementing Quantum Image Representation (QIR) methods.

QIR is a data embedding technique that provides an interface between classical and quantum platforms for representing digital images on quantum devices. Digital images typically have attributes such as pixel position and color information that can be encoded onto a quantum circuit using specific unitary transforms.

Understanding INEQR

While many QIR techniques exist, this article focuses on the Improved Novel Enhanced Quantum Representation (INEQR) method for image representation.

INEQR, introduced by Nan Jiang and Luo Wang², supports encoding non-square images with unequal horizontal (X) and vertical (Y) dimensions onto a quantum circuit.

INEQR employs unitary operations like Hadamard (H) and Controlled-NOT (CX) to capture the pixel position and color information, respectively. It utilizes the basis states of the qubits to represent this information, resulting in a deterministic image retrieval process. A significant limitation of INEQR is its inability to encode colored images.

A Little Math, Perhaps? Else, Skip to the Implementation! (Optional)

INEQR employs two unitary transforms:

1. Hadamard transform for encoding the pixel position.
2. Multi-CX transform for encoding the color information.

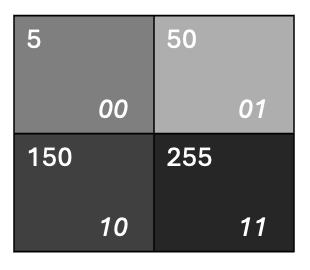
For simplicity, let us consider a grayscale image of size 2x2, with gray values in the range [0, 255].

Step 1:
The pixel positions of the four pixels in a 2x2 image can be represented in their binary formats as 00, 01, 10, and 11, which correspond to the coordinates of each pixel in the image grid:

• Top-left pixel corresponds to (Y = 0, X = 0)
• Top-right pixel corresponds to (Y = 0, X = 1)
• Bottom-left pixel corresponds to (Y = 1, X = 0)
• Bottom-left pixel corresponds to (Y = 1, X = 1)

INEQR utilizes a Hadamard transform that encodes these pixel positions on √4 = 2 qubits (q₀ and q₁).

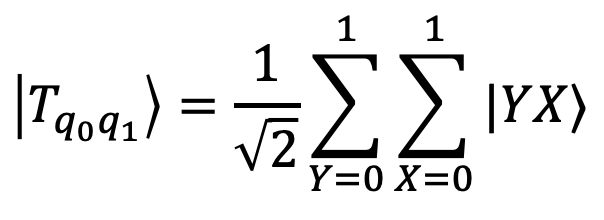
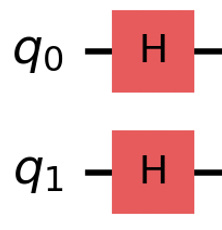
During practical implementation, Hadamard gates are followed by X gates, preparing an oracle-like structure for the multi-CX gates to encode color information corresponding to each pixel position.

Step 2:
The first action in this step is to convert the gray values in the range [0, 255] to their corresponding binary formats. For example, 50 in binary can be given as 00110010, and 255 as 11111111.

Now, a Multi-CX transform encodes the binary color information onto an additional 8 qubits (q₂ to q₉). For a 2x2 image, a CCX unitary gate, with controls on the first two positional qubits (q₀ and q₁), is applied to qubit qᵢ when the i-th color bit is 1.

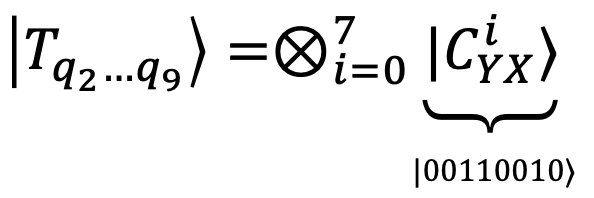
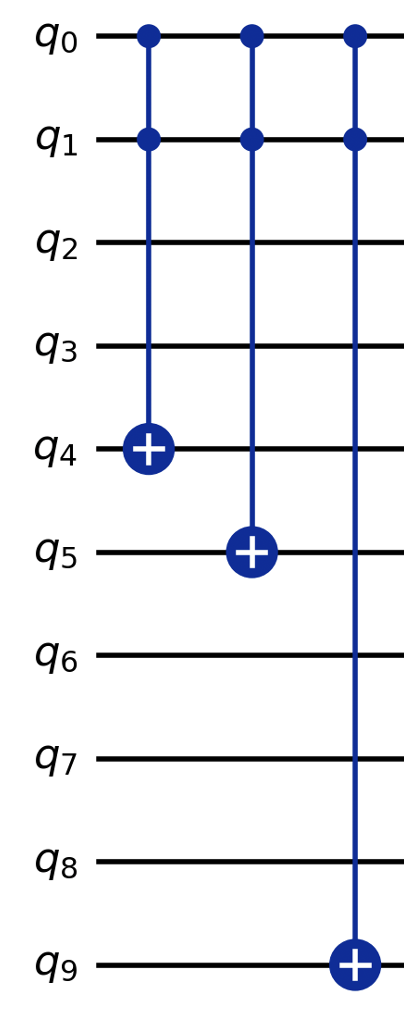
Combining the transforms in Step 1 and Step 2, an INEQR encoded 2x2 image can be given as:

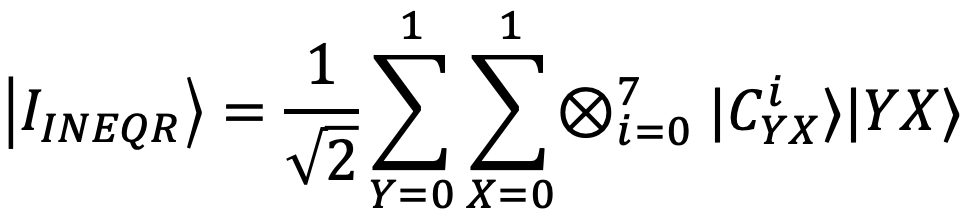
The total qubit requirement for INEQR is n₁ + n₂ + q. Remember, a generalized INEQR method can encode non-square images.

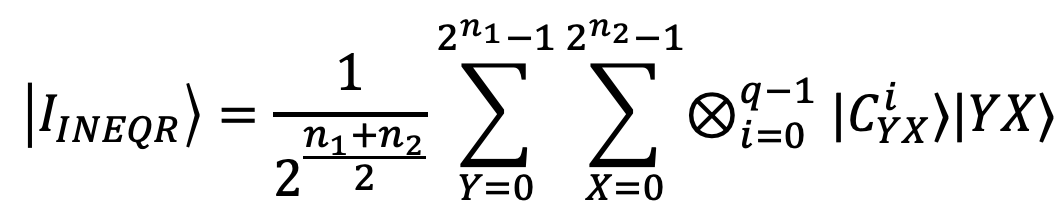
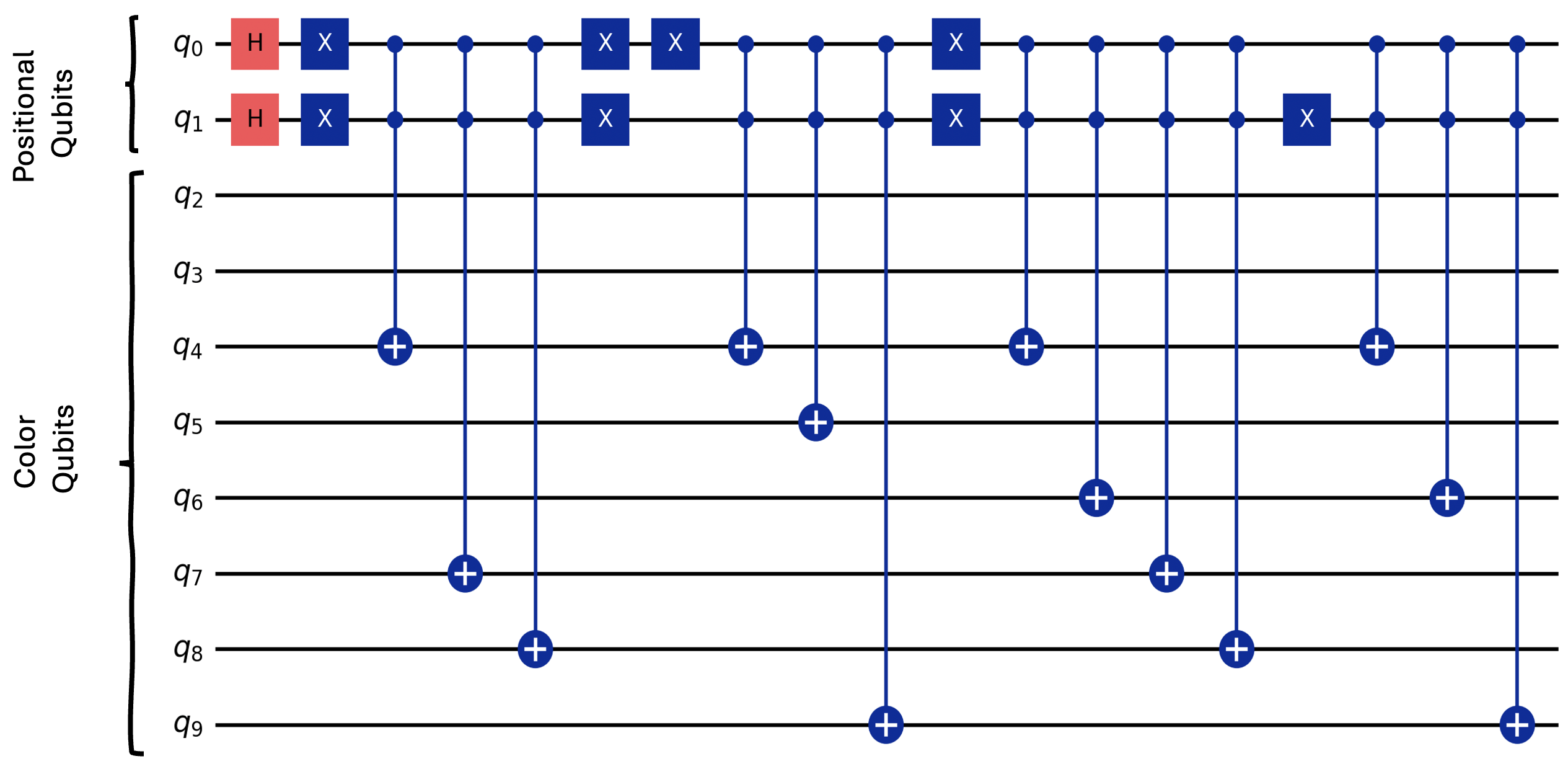
Implementation with piQture

piQture has an in-built implementation for INEQR in the image_representations module. Let us see how piQture can be utilized to build an INEQR embedding circuit.

Note: This implementation utilizes the load_mnist_dataset function from the data_loader module in piQture to import an MNIST dataset from PyTorch databases.

Alright, let us start by performing some imports.

import torch
from piqture.data_loader.mnist_data_loader import load_mnist_dataset
from piqture.embeddings.image_embeddings.ineqr import INEQR

Next, load the MNIST dataset using the load_mnist_dataset function.

# Resize images to 2x2
img_size = 2
train_dataset, test_dataset = load_mnist_dataset(img_size)

# Retrieve a single image from the dataset
image, label = train_dataset[1]
image_size = tuple(image.squeeze().size())

By default, the MNIST images are of the type tensor with float values. We transform these color values into integers and further to their binary representations.

# Change pixel values from tensor to list
pixel_vals = (image * 255).round().to(torch.uint8)
pixel_vals = pixel_vals.tolist()
print("Label: ", label, "\nPixel values: ", pixel_vals)

Finally, let us generate the INEQR circuit with piQture.

embedding = INEQR(image_size, pixel_vals).ineqr()
embedding.draw("mpl", style="iqp")

That is all for today. Stay tuned to the piQture repository for more intriguing implementations and the piQture-demos repository for upcoming demos and tutorials on QIR.